若无法得到车辆在地图上的准确位置及周围障碍物的位置,那么自动驾驶便无从谈起。因此在自动驾驶领域,对车辆自身及周围物体的精确定位至关重要。然而现实环境中存在各类噪声,无论是激光雷达、惯性导航器件甚至卫星定位系统都无法得到完全真实的车辆位置信息。为了应对此类情况,便需要采用滤波算法来过滤观测噪声,以得到更加精确的定位结果。
一、何为卡尔曼滤波
在各类滤波定位算法中,卡尔曼滤波是最为知名的一种。为了解决阿波罗登月计划中的航天器定位及噪声干扰问题,这种算法最初在1963年由匈牙利数学家鲁道夫·卡尔曼所提出[1]。卡尔曼滤波不仅将过去类似的基于系统可观性与可控性的控制方法做出了系统化的整理,并且在严格的数学意义上证明这种方法在线性系统的高斯随机噪声过滤方法中具有最优性。
卡尔曼滤波的简单举例
为了更好的理解卡尔曼滤波的基本原理,本文首先对卡尔曼滤波的原理进行举例说明。
试想一下,假设你要凭借地图从A地前往B地,你要如何知道自己的位置呢?
首先,你可以通过自己的脚程判断,“A地到B地大约10公里,凭我的脚程大约需要步行3小时左右”。
其次,还可以通过路牌和手里的地图判断,“这个路牌上写着到了D镇,地图上显示D镇应该在距离B地还有3公里的地方”。
然而不论是地图还是脚程估算都存在的较大误差,此时我们为了得到更准确的所处位置,可以结合地图与脚程来对当前位置进行估算。比如:A地到B地大约10公里,凭我的脚程大约需要步行3小时左右,目前已经走了2小时,那么我推测再过不久就可以到达D镇,此时再对照地图上D镇的位置,就可以得到更加精确的位置信息,同时通过对比实际到达D镇的时间,还可以反过来修正对于自己脚程的估计误差。
在这个例子里,通过自己脚程估计的位置,在卡尔曼滤波里就被称为状态预测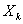 ,其误差则为估计误差
,其误差则为估计误差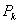 ,估计方法为预测矩阵
,估计方法为预测矩阵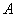 ,地图上自己的位置则为状态观测
,地图上自己的位置则为状态观测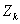 ,从地图换算到当前位置的方法则被称为观测矩阵
,从地图换算到当前位置的方法则被称为观测矩阵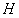 。卡尔曼的关键就在于对即将到来的观测进行预测,并用其对比最后实际得到的观测,通过这两者之间的差值进行修正。假设用一个笛卡尔坐标系来对这种方法进行表示,则可参考图1。
。卡尔曼的关键就在于对即将到来的观测进行预测,并用其对比最后实际得到的观测,通过这两者之间的差值进行修正。假设用一个笛卡尔坐标系来对这种方法进行表示,则可参考图1。
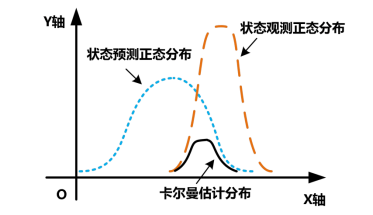 图1 卡尔曼滤波原理示意图
图1 卡尔曼滤波原理示意图
二、卡尔曼滤波的基本公式
根据上一节的例子,我们就可以引出卡尔曼滤波的基本公式:
 (1)
(1)
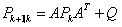 (2)
(2)
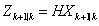 (3)
(3)
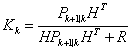 (4)
(4)
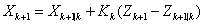 (5)
(5)
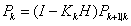 (6)
(6)
前两步是根据上一个最优估计值得出此刻的估计值和估计值的协方差,紧接着就可以得到此刻的最优估计值和最优估计值的协方差,然后利用此刻的最优估计值和最优估计值的协方差进行下一个迭代。
公式详解
看起来有点多,但是实际上非常紧凑,推理非常严谨,接下来将对上述六个公式进行详细解释。
首先式(1)为系统的状态预测公式,通过上一时刻的位置对当前时刻的位置进行了推测,但是由于过程噪声的存在,这个推测出的位置不完全符合真实情况。式(2)为系统的状态误差传递,类似式(1),是基于上一时刻位置可能分布的范围对当前时刻的可能分布范围做出预测,Q是可能的估计误差。式(3)则是当前时刻观测量的预测值,代表我们根据预测出的状态,推测出我们将会观测到的读数,并非真正的读数。式(4)为卡尔曼增益的计算方法,其物理意义为状态预测误差与观测误差的比例关系。式(5)则为对系统状态的更新,这个公式可以分为两方面看,后半段的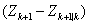 代表实际读数与推测读数之间的差值,被称为残差。使用式(4)求得的卡尔曼增益与残差相乘,可以得到对状态预测的修正量,最终式(5)可以得到图1中的卡尔曼位置估计更新。式(6)则为对位置估计的分布估计,可以作为下一时刻式(2)的初值使用。
代表实际读数与推测读数之间的差值,被称为残差。使用式(4)求得的卡尔曼增益与残差相乘,可以得到对状态预测的修正量,最终式(5)可以得到图1中的卡尔曼位置估计更新。式(6)则为对位置估计的分布估计,可以作为下一时刻式(2)的初值使用。
实例说明
假设车辆在进行匀速运动,则可以设置其递推运动模型为:
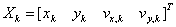 (7)
(7)
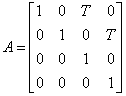 (8)
(8)
其中式(7)代表k时刻的车辆状态,包含车辆的坐标和在横纵坐标轴的速度,式(8)则为匀速运动状态转换矩阵,可以通过将式(7)、(8)带入式(1)求取下一时刻的状态预测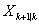 。
。
之后我们给出状态误差矩阵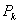 的迭代初值,通常设置为一个与状态同阶的单位阵,带入式(2)即可求得下一时刻的误差矩阵预测
的迭代初值,通常设置为一个与状态同阶的单位阵,带入式(2)即可求得下一时刻的误差矩阵预测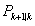 ,这里Q需要根据估计模型的误差来人为给定。
,这里Q需要根据估计模型的误差来人为给定。
下一步,我们假设运动系统使用GPS作为观测器,经过预处理的GPS信号可以直接输出车辆的位置坐标,那么GPS的观测模型可以简化为:
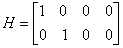 (9)
(9)
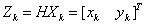 (10)
(10)
将式(9)与式(1)的结果带入式(3),可以得到基于状态预测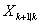 的观测值预测
的观测值预测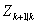 ,系统观测误差的方差矩阵R可以根据传感器的技术说明书确定。
,系统观测误差的方差矩阵R可以根据传感器的技术说明书确定。
最后,按顺序将上述变量带入式(4)、(5)、(6)即可实现对位置坐标的更新,同时得到的结果还可以作为下一步迭代的初值。
三、非线性卡尔曼滤波
虽然卡尔曼滤波已经在数学上被严格证明具有最优性,然而却无法处理非线性系统。针对这种情况,现有的解决方法分为两种,分别是基于泰勒展开进行线性化近似的扩展卡尔曼滤波[2]和基于多点采样进行均值方差近似的无迹卡尔曼滤波。
扩展卡尔曼滤波
扩展卡尔曼滤波通过一组式(11)所示的n阶泰勒线性展开式近似表达非线性函数:
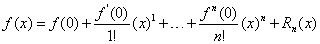 (11)
(11)
如图2所示,其阶数越高,近似程度越高。
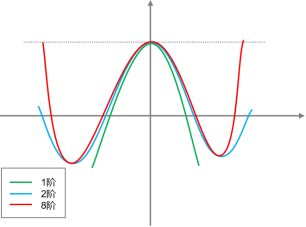 图2 各级泰勒展开线性化效果
图2 各级泰勒展开线性化效果
这种方法具有计算复杂度低、技术成熟的优点,因此,目前在工程中被广泛使用。然而由于泰勒展开式的复杂度随着阶数呈指数增长,往往在实际应用中很难实现三阶以上的泰勒展开,这导致了这种线性化方法存在较大的截断误差,因此限制了算法的估计精度,并且在非线性程度较高的系统中容易发散。
无迹卡尔曼滤波
无迹卡尔曼滤波则通过对非线性函数在目标时刻的均值与方法进行相似拟合来实现线性化近似的(如图3所示),这种方法被称为无迹变换(UT变换)。
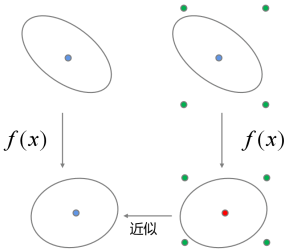 图3 无迹变换原理
图3 无迹变换原理
UT变换已被Julier和Uhlmann[3]证明具有不低于三阶泰勒展开的线性化精度,因此基于UT变换的无迹卡尔曼滤波具有相对于扩展卡尔曼滤波更高的精度,同时其均值与方差的拟合不会受函数非线性化程度的影响,因此可以适用于更为非线性的系统。然而,由于使用无迹卡尔曼滤波需要设置较多参数,并且计算负担较重,因此在实际工程中仍然不能完全取代扩展卡尔曼滤波。
基于上述原因,目前在非线性系统上需要根据系统特征与实际需求对滤波器的性能做出取舍,选择最合适的方法进行计算。
四、SLAM中的卡尔曼滤波与图优化
由于SLAM(Simultaneous Localization and Mapping,同步定位与建图)中对于特征点、路径与移动体的定位同卡尔曼滤波的适用范围十分吻合,因此,早期SLAM中通常采用卡尔曼滤波在后端对输出进行优化。随着计算能力的不断加强,近年来基于图优化的SLAM方法也逐渐占据了一席之地。
从应用角度分析,基于卡尔曼滤波和基于图优化的SLAM方法各有优势。
卡尔曼滤波具有计算速度快、系统简单的优点,但由于其对后端输出的优化仅基于相邻两个马尔可夫链的信息进行一次迭代,因此在精度上有所欠缺,更适用于高动态且对精度要求不高的场合。
相对的,因子图优化可以统筹全局信息以对各位姿输出进行优化,并且优化迭代次数可以人为设置,可以得到更加精确的后端输出。正因如此,其每次迭代及出现新的输出时都需要对全局进行计算,使得计算负担大幅增加。所以一般情况下,基于图优化的SLAM仅适用于对于精度要求极高的特殊场合。
随着技术的发展,这两种路线也在分别补齐自身的固有短板。
如基于滤波的SLAM中引入了迭代扩展卡尔曼滤波,将最小二乘法与卡尔曼滤波相结合,对误差而不是位姿进行优化,实现了更高的定位精度,并且可以实现动态设置迭代次数,代表算法有LINS和Fast-Lio等。
反之,为了应对图优化“牵一发而动全身”的问题,最近比较热门的LIOM和LIO-SAM等算法引入了动态滑窗和关键帧机制,仅对少数相关的时刻进行联系,有效降低了冗余计算,并且引入了IMU预积分等技术,进一步削减系统的计算负担,获得了更快的动态响应时间。
总体来看,基于图优化的SLAM是未来的发展趋势,而目前产品化的SLAM设备仍以滤波为主流。
参考文献
[1] Kalman R E. A New Approach to Linear Filtering and Predicition Problems[J]. Journal of Basic Engineering, 1960, 82(4): 35-35.
[2] Lekshmi B S , Susan S , Apren T J . Channel Estimation with Extended Kalman Filter for Fading Channels[J]. International Journal of Electronics Communication & Computer Technology, 2013, 3(5).
[3] Julier S J, Uhlmann J K. A New Extension of the Kalman Filter to Nonlinear Systems[J]. Proceedings of SPIE - The International Society for Optical Engineering, 1999, 3068:182-193.
(本文系赛目原创作品,如转载需注明出处。)